排序算法

先介绍一个网址：https://visualgo.net/zh/sorting

冒泡排序

依次比较相邻的两个数，不满足就交换位置

• 时间复杂度： O(n2)

• 空间复杂度：只涉及相邻元素的交换，是原地排序算法

• 算法稳定性：元素相等不会交换，是稳定的排序算法

时间复杂度是 O(n2)，看起来性能并不是很好，所以我们在实践中基本不会选用冒泡算法。

插入排序

插入排序的原理是：我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。

    /**
     * 插入排序实现函数（PHP）
     *
     * @param $nums
     * @return mixed
     */
    function insertion_sort($nums) {
        if (count($nums) <= 1) {
            return $nums;
        }

        for ($i = 0; $i < count($nums); $i++) {
            $value = $nums[$i];
            $j = $i - 1;
            for (; $j >= 0; $j--) {
                if ($nums[$j] > $value) {
                    $nums[$j + 1] = $nums[$j];
                } else {
                    break;
                }
            }
            $nums[$j + 1] = $value;
        }

        return $nums;
    }

• 插入排序需要两个嵌套的循环，时间复杂度是O(n2)；
• 没有额外的存储空间，是原地排序算法；
• 不涉及相等元素位置交换，是稳定的排序算法。

插入排序的时间复杂度和冒泡排序一样，也不是很理想，但是插入排序不涉及数据交换，从更细粒度来区分，性能要略优于冒泡排序。

选择排序

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。图示如下：

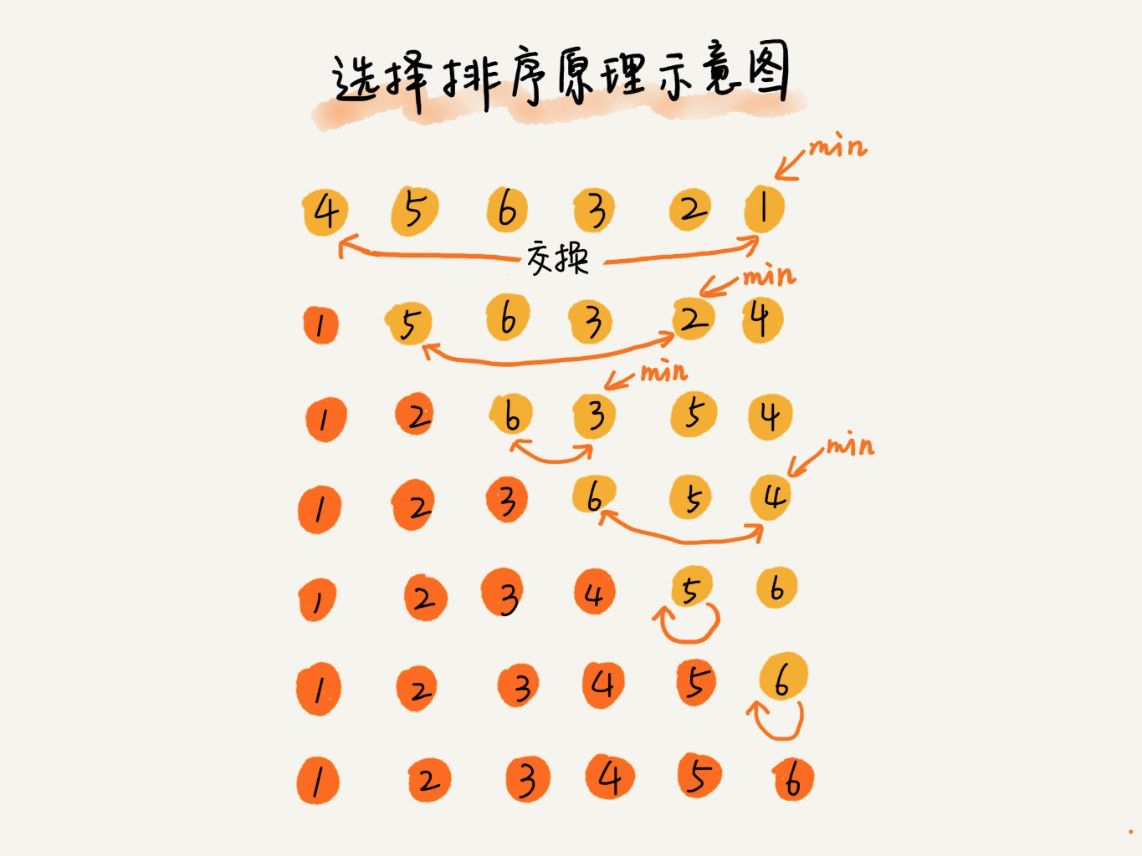
<?php

    /**
     * 选择排序算法实现
     */
    function selection_sort($nums)
    {
        if (count($nums) <= 1) {
            return $nums;
        }

        for ($i = 0; $i < count($nums); $i++) {
            $min= $i;
            for ($j = $i + 1; $j < count($nums); $j++) {
                if ($nums[$j] < $nums[$min]) {
                    $min = $j;
                }
            }
            if ($min != $i) {
                $temp = $nums[$i];
                $nums[$i] = $nums[$min];
                $nums[$min] = $temp;
            }
        }

        return $nums;
    }

    $nums = [4, 5, 6, 3, 2, 1];
    $nums = selection_sort($nums);
    print_r($nums);

归并排序

所谓归并排序，指的是如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

归并排序使用了分治思想，分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。说到这里，可能你就能联想起我们之前讲到的一个编程技巧 —— 递归，没错，归并排序就是通过递归来实现的。这个递归的公式是每次都将传入的待排序数组一分为二，直到不能分割，然后将排序后序列合并，最终返回排序后的数组。

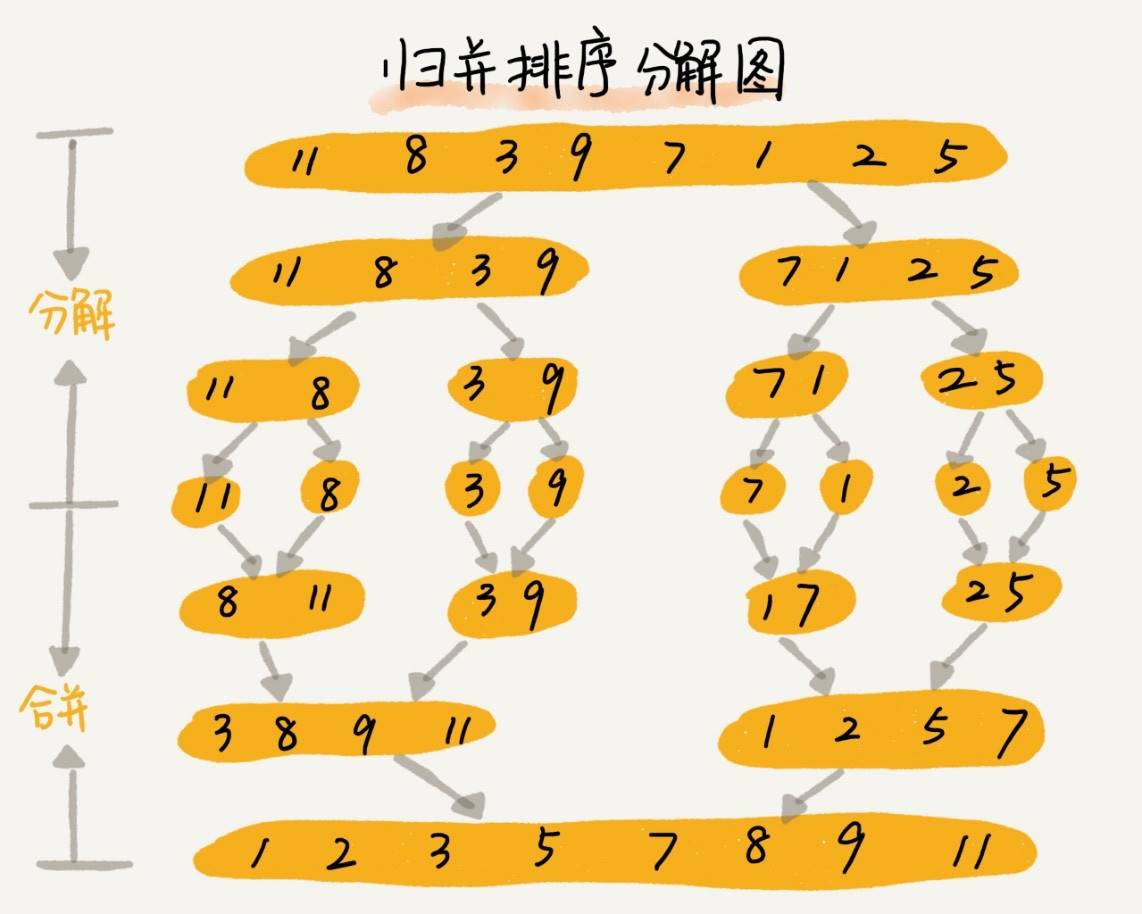
<?php
    function merge_sort($nums)
    {
        if (count($nums) <= 1) {
            return  $nums;
        }

        merge_sort_c($nums, 0, count($nums) - 1);
        return $nums;
    }

    function merge_sort_c(&$nums, $p, $r)
    {
        if ($p >= $r) {
            return;
        }

        $q = floor(($p + $r) / 2);
        merge_sort_c($nums, $p, $q);
        merge_sort_c($nums, $q + 1, $r);

        merge($nums, ['start' => $p, 'end' => $q], ['start' => $q + 1, 'end' => $r]);
    }

    function merge(&$nums, $nums_p, $nums_q)
    {
        $temp = [];
        $i = $nums_p['start'];
        $j = $nums_q['start'];
        $k = 0;
        while ($i <= $nums_p['end'] && $j <= $nums_q['end']) {
            if ($nums[$i] <= $nums[$j]) {
                $temp[$k++] = $nums[$i++];
            } else {
                $temp[$k++] = $nums[$j++];
            }
        }

        if ($i <= $nums_p['end']) {
            for (; $i <= $nums_p['end']; $i++) {
                $temp[$k++] = $nums[$i];
            }
        }

        if ($j <= $nums_q['end']) {
            for (; $j <= $nums_q['end']; $j++) {
                $temp[$k++] = $nums[$j];
            }
        }

        for ($x = 0; $x < $k; $x++) {
            $nums[$nums_p['start'] + $x] = $temp[$x];
        }
    }

    $nums = [4, 5, 6, 3, 2, 1];
    $nums = merge_sort($nums);
    print_r($nums);

快速排序

大名鼎鼎的 快排 快排的核心思想是这样的：

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

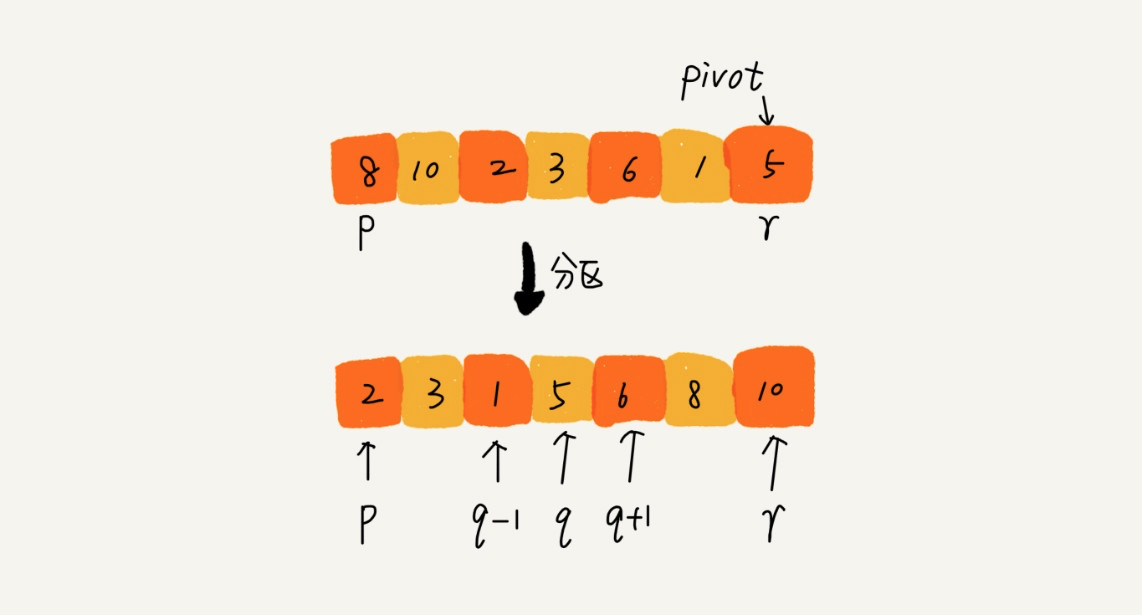
根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了，而且你可以看到我们不需要像归并排序那样做合并操作，也就不需要额外的内存空间，在算法复杂度和归并排序一样的情况下，有着更好的空间复杂度表现。

快速排序首先要找到分区点 pivot，一般我们会将数组最后一个元素或者第一个元素作为 pivot，比如我们以最后一个元素作为分区点，然后通过两个变量 i 和 j 作为下标来循环数组，当下标 j 对应数据小于 pivot 时，交换 i 和 j 对应数据，并且将 i 往前移动一位，否则 i 不动，下标 j 始终是往前移动的，j 到达终点后，将 pivot 与下标 i 对应数据交换，这样最终将 pivot 置于数组中间，[0...i-1] 区间的数据都比 pivot 小，[i+1...j] 之间的数据都比 pivot 大，我们以递归的方式处理该流程，最终整个数组都会变成有序的，对应的算法操作流程如下：

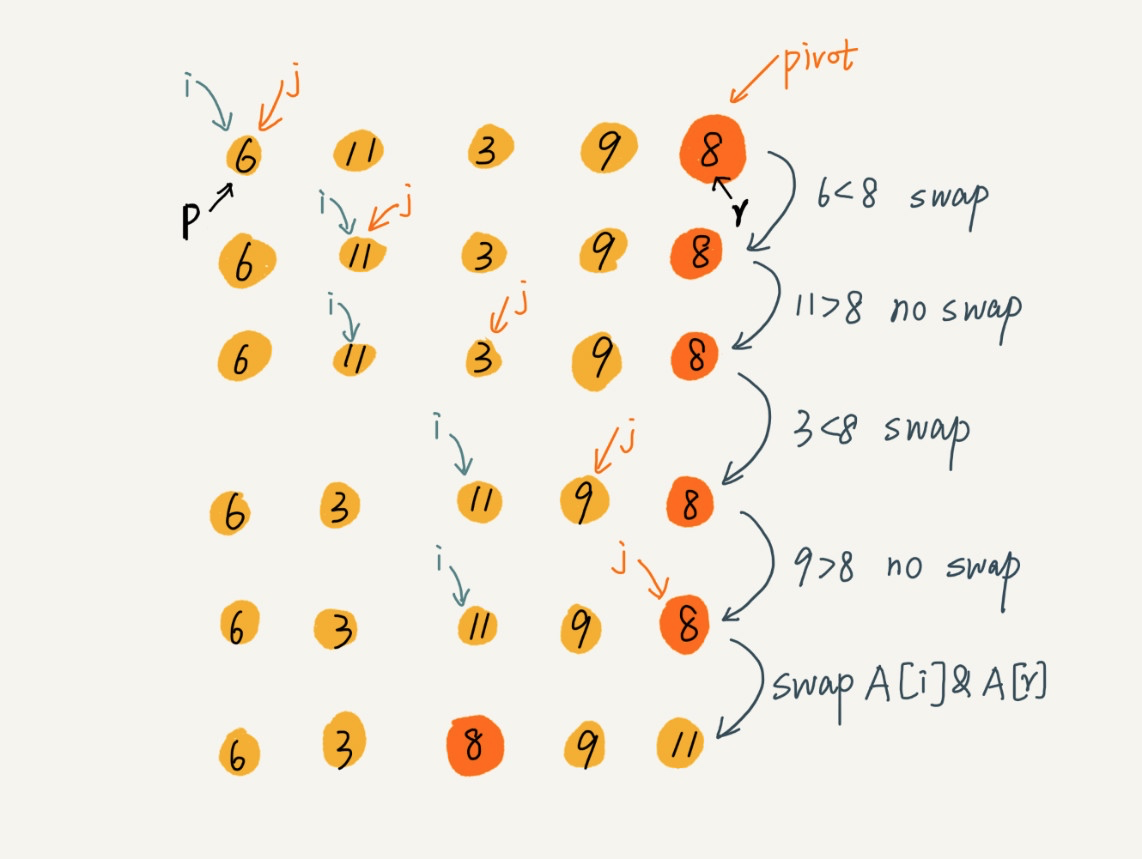
示例代码：

<?php
    
    function quick_sort($nums)
    {
        if (count($nums) <= 1) {
            return $nums;
        }
    
        quick_sort_c($nums, 0, count($nums) - 1);
        return $nums;
    }
    
    function quick_sort_c(&$nums, $p, $r)
    {
        if ($p >= $r) {
            return;
        }
    
        $q = partition($nums, $p, $r);
        quick_sort_c($nums, $p, $q - 1);
        quick_sort_c($nums, $q + 1, $r);
    }
    
    // 寻找pivot
    function partition(&$nums, $p, $r)
    {
        $pivot = $nums[$r];
        $i = $p;
        for ($j = $p; $j < $r; $j++) {
            // 原理：将比$pivot小的数丢到[$p...$i-1]中，剩下的[$i..$j]区间都是比$pivot大的
            if ($nums[$j] < $pivot) {
                $temp = $nums[$i];
                $nums[$i] = $nums[$j];
                $nums[$j] = $temp;
                $i++;
            }
        }
    
        // 最后将 $pivot 放到中间，并返回 $i
        $temp = $nums[$i];
        $nums[$i] = $pivot;
        $nums[$r] = $temp;
    
        return $i;
    }
    
    $nums = [4, 5, 6, 3, 2, 1];
    $nums = quick_sort($nums);
    print_r($nums);

• 性能分析 正如我们前面所说的，快速排序是原地排序算法，时间复杂度和归并排序一样，也是 O(nlogn)，这个时间复杂度数据量越大，越优于 O(n2)，但是快速排序也有其缺点，因为涉及到数据的交换，有可能破坏原来相等元素的位置排序，所以是不稳定的排序算法，尽管如此，凭借其良好的时间复杂度表现和空间复杂度的优势，快速排序在工程实践中应用较多，比如 PHP 数组的 sort 函数底层就是基于快速排序来实现的

PHP sort 函数底层实现分析

PHP 源码地址：https://github.com/php/php-src