主串:给定的原始字符串
模式串:需要查找的串
例如:需要在字符串 A 中,查找 B 字符串,那么 A 就是主串,B 就是模式串
BF 算法
BF 算法就是暴力匹配算法,挨个去比较,不相等就将整个模式串后移一位,继续比较

KMP 算法
算法的核心思想
假设主串是a,模式串是 b。在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,我们希望找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况,从而避免 BF 算法这种暴力匹配,提高算法性能。下面我们来探讨下这个规律如何找到。
参考下面个主串和模式串的匹配,当模式串移动到当前位置,比对到最后一个字符 D 时,发现与主串不匹配,如果按照 BF 算法,就是把模式串往后移一位,再逐个比较,这样做固然可以,但是效率很差:

一个基本事实是,当 D 与主串不匹配时,我们已知前面的主串序列是 ABCDA,如果把模式串往后移一位肯定和主串不匹配,我们可不可以直接把模式串移到下一个可能和 A 匹配的主串位置?
实际上,KMP 算法正是基于这一理念,设法利用这个已知信息,不把模式串移到已经比较过的位置,继续把它向后移,这样综合下来就极大提高了搜索匹配效率。
怎么找到这个规律,确定把模式串往后移多少位呢?在模式串和主串匹配的过程中,我们把不能匹配的那个字符仍然叫作「坏字符」,把已经匹配的那段字符串叫作「好前缀」:
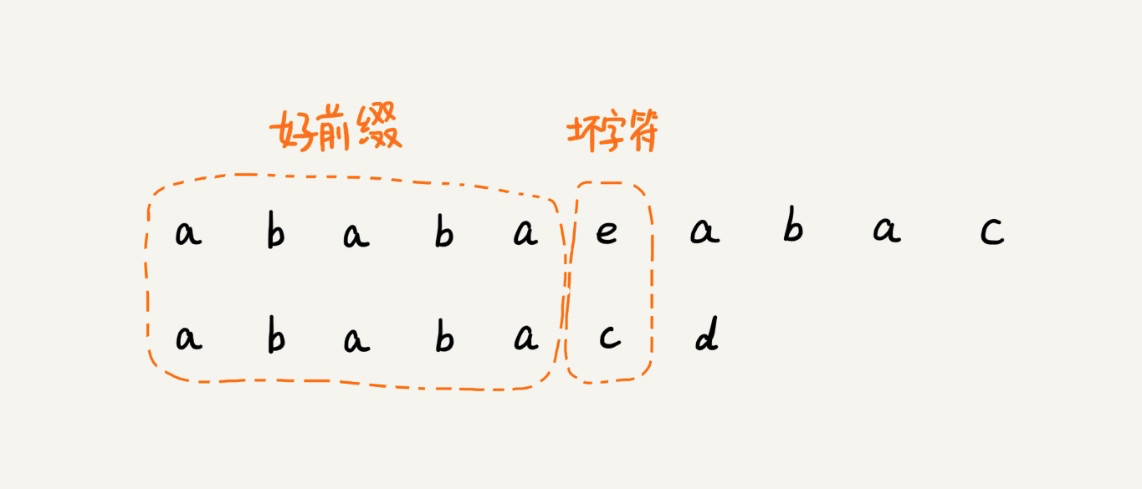
在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,我们只需要拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的下标位置,然后将模式串后移到该位置即可。
这里,我们要解释几个概念:
-
后缀子串:以某个字符串最后一个字符为尾字符的子串(不包含字符串自身),比如上面的 ababa,后缀子串为 baba、aba、ba、a;
-
前缀子串:以某个字符串第一个字符为首字符的子串(不包含字符串自身),还是以 ababa 为例,前缀子串为 a、aba、abab;
-
最长可匹配后缀子串:后缀子串与前缀子串最长可匹配子串,也可叫做共有子串,以 ababa 为例,自然是 aba 了,长度为 3;
-
最长可匹配前缀子串:与上面定义相对,即前缀子串与后缀子串最长可匹配子串。最长可匹配前缀子串和最长可匹配后缀子串肯定是一样的。
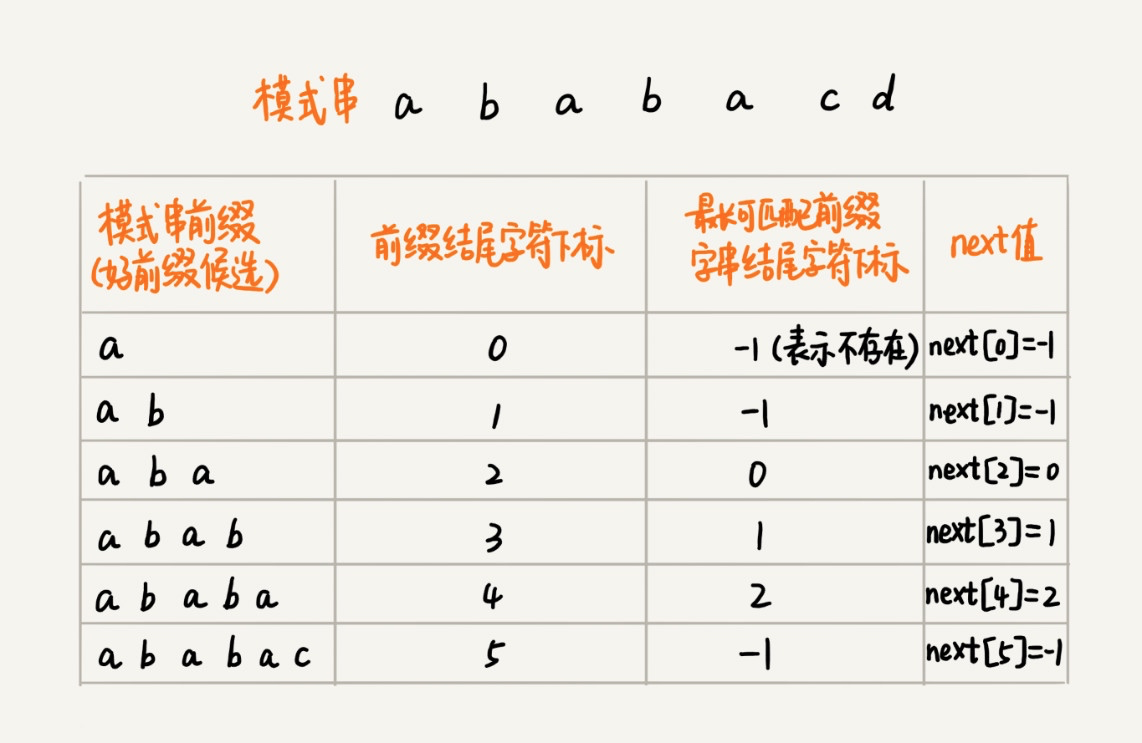
假设坏字符所在位置是 j,最长可匹配后缀子串长度为 k,则模式串需要后移的位数为 j-k。每当我们遇到坏字符,就将模式串后移 j-k 位,直到模式串与对应主串字符完全匹配;如果移到最后还是不匹配,则返回 -1。这就是 KMP 算法的核心思想。
KMP 算法的实现
先留个坑
Trie 树的定义、实现及应用
Trie 树的定义
Trie 树,也叫「前缀树」或「字典树」,顾名思义,它是一个树形结构,专门用于处理字符串匹配,用来解决在一组字符串集合中快速查找某个字符串的问题。
注:Trie 这个术语来自于单词「retrieval」,你可以把它读作 tree,也可以读作 try。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起,比如我们有["hello","her","hi","how","seo","so"] 这个字符串集合,可以将其构建成下面这棵 Trie 树:
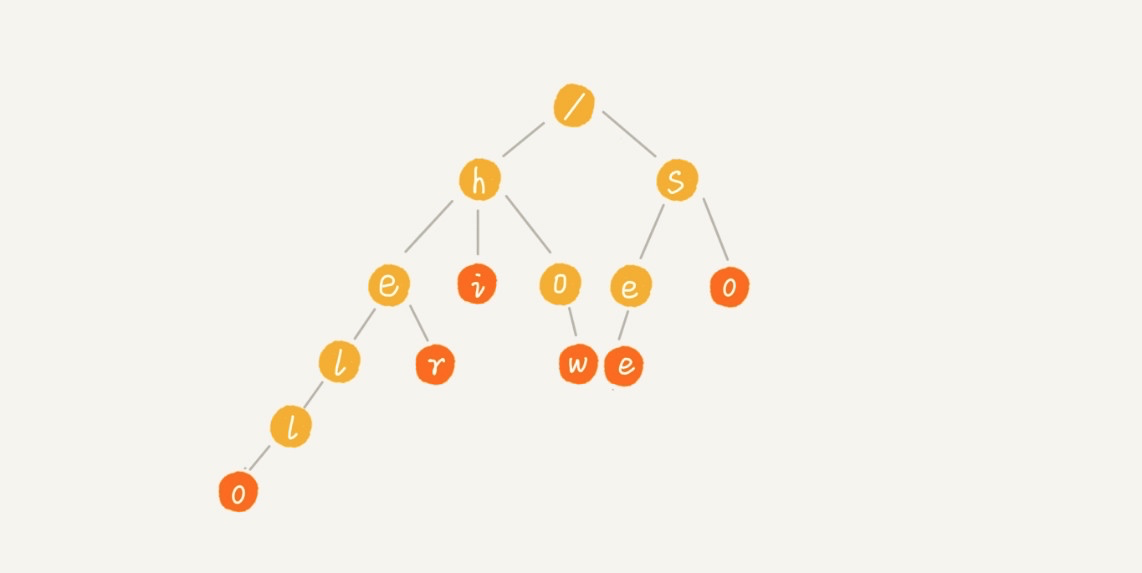
每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(红色节点表示是某个单词的结束字符,但不一定都是叶子节点)。
这样,我们就可以通过遍历这棵树来检索是否存在待匹配的字符串了,比如我们要在这棵 Trie 树中查询 her,只需从 h 开始,依次往下匹配,在子节点中找到 e,然后继续匹配子节点,在 e 的子节点中找到 r,则表示匹配成功,否则匹配失败。通常,我们可以通过 Trie 树来构建敏感词或关键词匹配系统。
Trie 树的实现
Trie 树的复杂度
Trie 树的应用
-
敏感词过滤系统
-
搜索框联想功能
-
进而可以扩展到浏览器网址输入自动补全、IDE代码编辑器自动补全、输入法自动补全功能等。
字符串匹配函数 strstr 底层实现原理剖析
PHP 提供的字符串匹配函数多是单模式匹配,因此大多通过 KMP 算法实现
链接地址:https://xueyuanjun.com/post/21001